侾丏偼偠傔偵
丂悢妛偺庼嬈傪彮偟偱傕恎嬤側傕偺偵姶偠偝偣偨偄偲僐儞僺儏乕僞傪巊偭偨庼嬈傪巒傔偰20擭偵側傝傑偡丅
丂PC9801 BASIC僾儘僌儔儉偺帺嶌丆VB偵傛傞WindowsCAI媦傃悢妛僣乕儖Mathematica側偳偺丆旕擔忢偲偟偰偺僐儞僺儏乕僞偵傛傞妛廗偼桳岠側傕偺偱偟偨丅
丂乽屄恖儂乕儉儁乕僕乽師戙偺偙偳傕偨偪傊乿 http://www2h.biglobe.ne.jp/~zidai/ 傊僾儘僌儔儉傪宖嵹偟偰偍傝傑偡丅嫵堢梡僼儕乕僂僃傾偲偟偰偁傝傑偡偺偱丄帋摦偟偰偄偨偩偗傟偽岾偄偱偡丅
丂嶐擭搙丄俁擭偱偺悢嘨偺庼嬈偺拞偱傢偨偟偼丄惗搆偨偪偵乽娭悢幃偐傜僌儔僼偺偍偍傛偦偺宍傪憐憸偱偒側偄偐丆偦傫側椡傪彅孨偵偼恎偵偮偗偰傎偟偄丅乿偲尵偄懕偗偰偒傑偟偨丅
丂偦傫側偲偒乽僌儔僼偑摦偔偲悢妛偼妝偟偄乿偲戣偡傞乽娭悢僌儔僼僜僼僩GRAPES僷乕僼僃僋僩僈僀僪乿偲偄偆CD-ROM晅偒偺杮(桭揷彑媣挊 暥塸摪1800墌)偵弌夛偄傑偟偨丅
丂戝嶃嫵堢戝妛晬懏崅摍妛峑抮揷峑幧偺桭揷彑媣巵偵傛傞僼儕乕僂僃傾偺悢妛僾儘僌儔儉偱偡丅
丂娭悢幃傪梌偊傞偲帺摦揑偵僌儔僼傪昤偄偰偔傟傑偡丅MS-DOS帪戙偺GRAPES傪摦偐偟偨偙偲傕偁傝傑偟偨偐傜丄尰応偱嶌偭偨偒傔嵶偐偄僜僼僩偱偁傞偙偲傪抦偭偰偄傑偟偨丅
丂桭揷巵偺儂乕儉儁乕僕乮http://www.osaka-kyoiku.ac.jp/~tomodak/)丂偱偼條乆側庼嬈椺偑宖嵹偝傟偰偄傑偡丅
丂杮峑偱偼乽亙妛傃偨偄亜傪堢偰傞怴僇儕僉儏儔儉乿偲偟偰丄俁擭慜偐傜懡條側慖戰傪攝抲偟偨庼嬈夵妚傪巒傔偰偄傑偟偨丅乮導擈儂乕儉儁乕僕丂http://www.hyogo-c.ed.jp/~kenama-hs/sinkatei/乯
丂侾擭師偵侾帪娫偺忣曬婎慴傪慡堳偵廋摼偝偣丄俀擭師偐傜偼乽忣曬壢妛椶宆乿偱偺13扨埵偵媦傇忣曬娭楢庼嬈側偳摿怓偁傞僇儕僉儏儔儉傪攝抲偟偰偄傑偡丅
丂Mathematica傪僀儞僗僩乕儖偟偨Windows98僐儞僺儏乕僞幒傕偁傞偺偱偡偑丄忣曬娭楢偺庼嬈偱偄偭傁偄偵媗傑偭偰偄偰悢妛偺庼嬈偵巊偊傞梋抧偑偁傝傑偣傫偱偟偨丅
丂偟偐偟偙偺GRAPES側傜丄斾妑揑嬻偄偰偄傞Windows95攝旛偺戞俀僐儞僺儏乕僞幒偱傕巊偊傑偡丅
偙傟傑偱旝暘朄傪巊偭偰憹尭昞傪嶌傝僌儔僼偺奣棯傪昤偄偰偒傑偟偨偑丆偙偺僜僼僩偱娭悢幃傪懪偪崬傓偩偗偱僌儔僼偑栚偺慜偵昞帵偝傟傞偙偲傪懳斾偝偣傟偽偒偭偲棟夝偑怺傑傝傑偡丅
丂惗搆偨偪偵丄悢嘨偱妛傫偱偒偨條乆側娭悢僌儔僼傪尒偣傞偙偲偑偱偒傞丄偆傟偟偄偙偲偱偡丅媫偓弨旛傪巒傔丄俀妛婜偺廔傢傝偵侾帪娫偺庼嬈傪慻傓偙偲偲側傝傑偟偨丅
丂2001擭12寧18擔丄俁妛擭帺慠壢妛椶宆慖戰惗搆30柤傊偺悢嘨偺庼嬈偱偡丅
俀丏庼嬈埬偲庼嬈夁掱
乮侾乯乽娭悢僌儔僼僜僼僩GRAPES偱娭悢傪尒傞両乿偲戣偟偨庼嬈僾儕儞僩偺攝晍
丂僌儔僼僜僼僩乽GRAPES乿傪婲摦偝偣傑偡丅
丂埻傫偩斖埻偺奼戝傗弅彫傗堏摦偑偱偒傞偙偲傪愢柧偟丄偦偺傾僀僐儞傪偒偪傫偲妋擣偟偰偍偒傑偡丅
丂傑偢乽GRAPES偺偍偍傛偦偺婡擻偲憖嶌曽朄乿傪妛傇偨傔偵丆乽娭悢偺嬌尷乿偺椺偲偟偰傛偔巊傢傟傞乽y=sin倶偲y=tan倶偑倶佮0偱偼y=倶偲堦抳偡傞乿偙偲傪挷傋傑偡丅
丂y1=sin倶丆y2=tan倶丆y3=倶偺俁偮偺娭悢幃傪擖椡偟偰俁怓偺僌儔僼傪昤偒傑偡丅
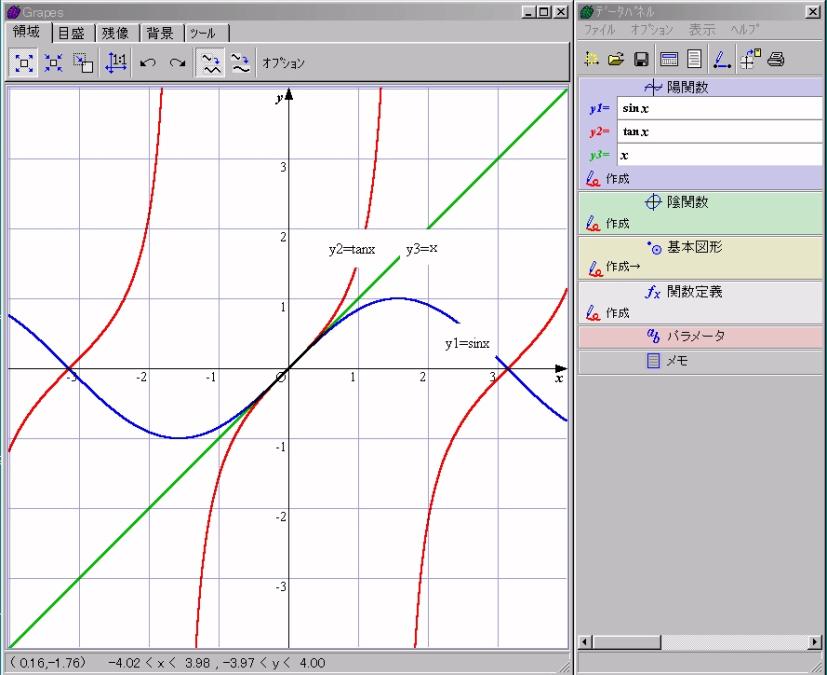
丂偦偟偰尨揰晅嬤偺彫偝側椞堟傪奼戝偡傞偲丆俁杮偺僌儔僼偑嬤帡偟偰偄傞偙偲偑栚偺慜偵昞帵偝傟傑偡丅
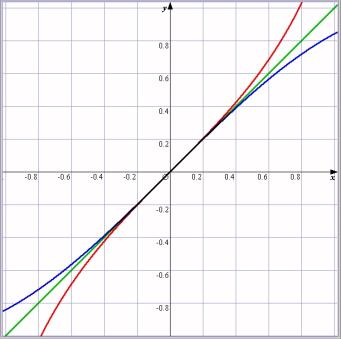
丂悢妛揑偵尵偆偲乽俁偮偺娭悢偼x=0偵偍偗傞嬌尷偱偼摍偟偄偲偟偰椙偄乿偲偄偆栤戣夝朄偺僥僋僯僢僋偑妋偐傔傜傟傑偡丅
丂嵟弶偼丄斖埻傪奼戝昞帵偡傞偺偵戝傢傜傢偱偡偑丄偡偖偵側傟偰偄偒傑偡丅屳偄偵嫵偊偁偄傪偟偰偔傟傑偡丅尨揰晅嬤偱俁杮偑摨偠捈慄偵尒偊傞偙偲偑帇妎揑偵妋偐傔傜傟傑偟偨丅
乮俀乯僌儔僼偺奣棯傪梊憐偟傛偆
丂師偺壽戣偼乽娭悢偺僌儔僼偺奣棯傪偮偐傔傞傛偆偵側傠偆丅憹尭昞傪彂偐側偔偰傕僌儔僼偑梊憐偱偒側偄偩傠偆偐丠乿偲偄偆僥乕儅偱偡丅
丂嫵壢彂偵弌偰偒偨乽俁師娭悢丄係師娭悢偺僌儔僼偺奣棯乿偺栤戣偱偡丅
丂傑偢乽係師娭悢 y亖x^4亅4x^2偺僌儔僼偺奣棯偼丠乿偱偡丅墧昅彂偒偱塃偺埻傒偵丄乽x^2(x亄2)(x亅2)亖0傛傝廳夝x亖0偲x亖2,亅2乿偲僸儞僩傪彂偄偰偍偒傑偡丅
丂偙偺乽巻偲墧昅乿偺寁嶼傛傝丄僌儔僼偺奣棯傪梊憐偱偒傑偣傫偐丠偲栤偄偐偗傑偡丅
丂乽巻偲墧昅乿偺僾儕儞僩晹暘偼偄偭偝偄撉傑偢偵丄傂偨偡傜娭悢幃傪擖椡偟偰丄僌儔僼昞帵偩偗偡傞惗搆偑弌偰偒傑偡丅僽儗乕僉偼偐偗傑偡偑丄僌儔僼昞帵偵枺偣傜傟偰偄傞偺偱偁傟偽丄偦傟偼偦傟偱偄偄偙偲偩偲巚偄傑偡偺偱丄偦偺傑傑偵偟偰偍偒傑偡丅
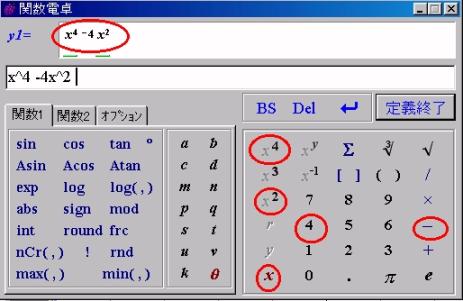
丂婥偺憗偄惗搆偼傕偆擖椡偟偰偄傑偡丅
丂擖椡偼忋偺傛偆側乽娭悢揹戩乿偑梡堄偝傟偰偍傝丄師乆偲塸悢帤傪墴偟偰偄偗偽娭悢幃偑嶌傜傟傑偡丅
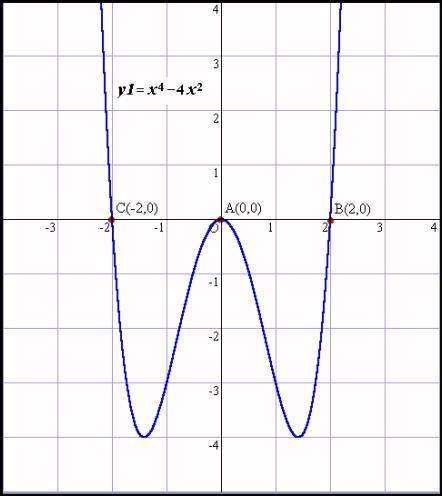
丂偡傞偲弖帪偵係師幃偺僌儔僼偑昤偐傟傑偡丅
丂巻偲墧昅偺寁嶼偐傜丄乽x^2(x亄2)(x亅2)亖0傛傝廳夝x亖0偲x亖2,亅2乿偲偟偨寁嶼偺堄枴傪偙偙偱揱偊傑偡丅
丂師偓偵乽俁師娭悢 y亖乮x亄2乯^2乮x亅3乯偺僌儔僼偺奣棯偼丠乿傪弌戣偟傑偡丅
丂偡偱偵帋尡栤戣側偳偱弌夛偭偰偄傞幰偼梕堈偵偦偺奣棯傪棟夝偟偰偄偒傑偡丅
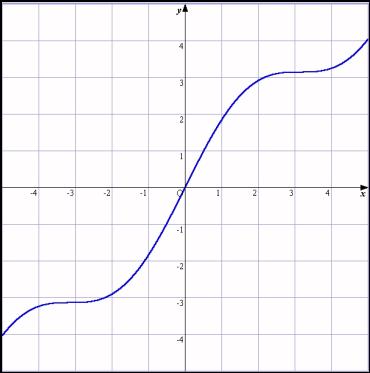
丂偝偁師偼丄乽y亖x+sin倶乿偺僌儔僼偺梊憐偱偡丅
丂偙偺僌儔僼偼y亖x偺忋偵sin倶偺攇傪廳偹偨傕偺偱偁傞偙偲偑丄嵟弶暘偐傜側偔偰傕丄弅彫偟偨恾傪尒傟偽傢偐偭偰偔傟傞偺偱偼偲婜懸偟傑偡丅
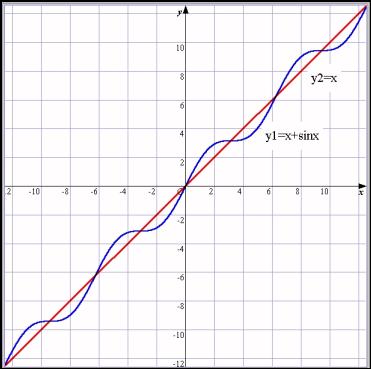
丂夞傝側偑傜丄壓偺恾偺塃偺僌儔僼偺傛偆偵昞帵偝傟偨惗搆偵丄乽45亱偺捈慄y亖x偺忋偵怳摦偡傞sinx偑偺偭偐偭偰傞傫傗偱乿偲榖偡偲丄偦偆偐偲擺摼偟偰偔傟傑偡丅
 丂
丂
丂乽娭悢幃偐傜僌儔僼偺奣棯傪梊憐偡傞椡傪偮偗偨偄乿偲偄偆庼嬈幰偺堄恾偑揱傢偭偨偱偟傚偆偐丅
乮俁乯寁嶼偱愙慄偺曽掱幃傪媮傔丆夋柺偱妋偐傔傛偆
丂婜枛峫嵏偵弌偟偨乽y亖x^3+x^2亅1忋偺揰 (亅1,亅1) 偵偍偗傞愙慄偺曽掱幃傪媮傔傛乿偺栤戣
偺摎偊偑乽y亖x乿偱偁偭偨偙偲傪揱偊偰丆偦傟傪夋柺偱妋偐傔偝偣傑偡丅
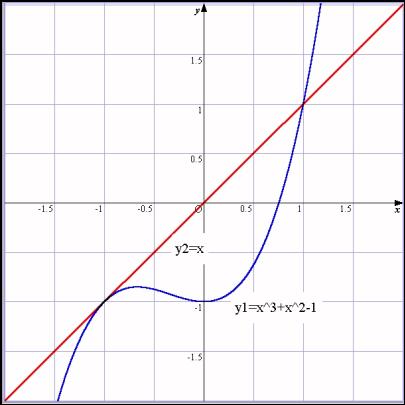
丂峏偵丄偄偔偮偐愙慄偺栤戣傪昞帵偟傑偡丅
丂愙揰晅嬤傪奼戝偟偰偄偔偲乽愙偟偰偄傞乿偙偲偑帇妎揑偵妋擣偱偒傑偡丅
丂僾儕儞僩偵偼丄庤彂偒偱偦偺乽夝摎乿傪彂偄偰偍偒傑偡丅
乮係乯敪揥偲偟偰丆嶰妏娭悢偺僌儔僼
丂悢嘨偵弌偰偒偨娭悢偺僌儔僼壽戣傪傗傝偁偘偰偟傑偭偨惗搆偨偪傊丄敪揥偲偟偰丄扨怳摦偺崌惉側偳傪乽GRAPES乿偱尒偣偰偁偘偨偄偲巚偄傑偡丅
丂傑偢y亖3sin倶+4cos倶 偑偒傟偄側惓尫攇偱偁傞偙偲傪尒偣丆怳暆偑俁亄係亖俈偱偼側偔俆偱偁傞偙偲傪拲帇偝偣傑偡丅峏偵庴尡偵偄偮傕弌偰偔傞 y亖sin倶+cos倶偑 y亖併俀sin(倶亄兾/係)偱偁傞偙偲傪尒偣傑偡丅
丂師偓偵y亖Asin(Bx)偺僷儔儊乕僞A,B傪偄傠偄傠曄偊偰丄A偑攇偺怳暆丄B偑攇偺怳摦悢偵偁偨傞偙偲傪帇妎揑偵偮偐傑偣傑偡丅
丂乽嶰妏娭悢偺僌儔僼乿偺妛廗暘栰偼丄惗搆偨偪偑嬯庤偲偡傞晹暘偱偡丅偙偆偟偰娭悢幃偺僷儔儊乕僞傪偳傫偳傫曄偊偰偄偔偙偲偱丄乽幃偑恾宍傪憂傞乿偲偄偆姶妎傪摼偰偔傟傞偺偱偼偲婜懸偟偰偺嶌嬈偱偡丅
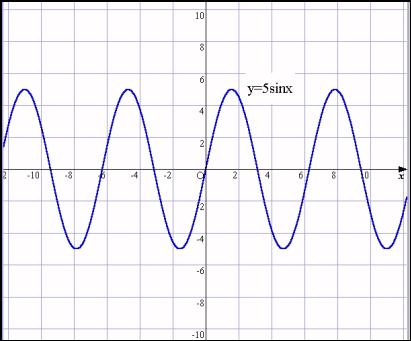
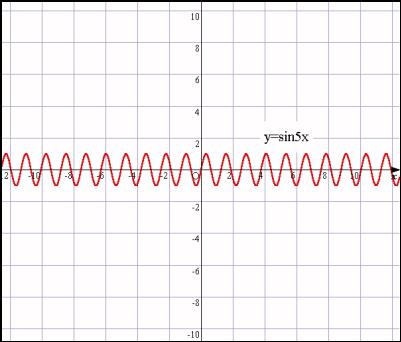
丂嫵幒傊栠偭偰崟斅庼嬈傪偟偨偲偒丄y亖sin俆x偲偡傟偽側偤怳摦偑俆攞寖偟偔側傞偺偐傪乽偨偲偊偽倶偑10亱曄壔偟偨偩偗偱丄俆攞偺50亱曄壔偟偨偙偲偵側傝寖偟偄怳摦傪偡傞偙偲偵側傞乿偲愢柧偟偨偲偒丄惗搆偨偪偼偙傟傑偱傛傝偢偭偲暘偐偭偰偔傟傞偺偱偼側偄偐偲婜懸偟傑偡丅
 丂
丂
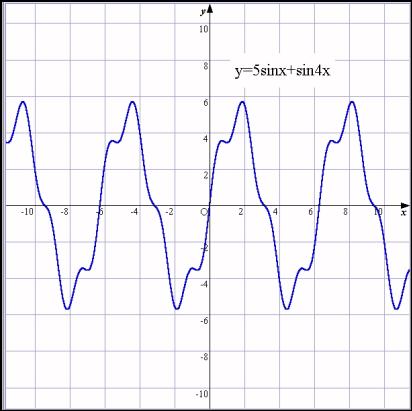
丂嵟屻偵y亖5sin倶亄sin4x側偳偱偆偹傝偺偁傞攇宍傪嶌傜偣丆乽僔儞僙僒僀僓乕偱壒傪嶌傠偆乿偺壽戣偱掲傔偔偔傝偱偡丅
 丂
丂
丂乽偙傟偑壒傪弌偡僔儞僙僒僀僓乕側傫偐偵巊傢傟偰偄傞棟榑側傫偱偡傛乿偲榖偟傑偡偲丄乽僼乕儞乿偲姶怱偟偰暦偄偰偔傟傞惗搆偑弌偰偒傑偡丅
丂偙偙傑偱偔傟偽嬯楯偟偰弨旛偟偨峛斻偑偁偭偨偲偄偆傕偺偱偡丅
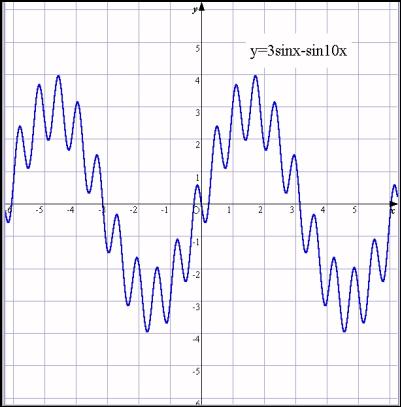
丂崟斅偵僶僀僆儕儞偺傛偆側攇宍傪昤偒丆偙傟偲帡偨攇宍傪偮偔傝側偝偄丆偲栤戣傪弌偟傑偡丅
丂25柤拞俇柤偑庢傝偐偐傞偙偲偑偱偒丆婔恖偐sin10x側偳偱嵶偐側曄壔偵挧愴偟偰偄傑偟偨丅
俁丏惗搆偼妛傃偨偑偭偰偄傑偡
丂師偺擔丄庼嬈偺傾儞働乕僩傪庢傝傑偟偨丅夞摎悢俀俆柤丅
丂乽亂侾亃偳偙傑偱恑傒傑偟偨偐乿偵懳偟偰偼丄
丂丂丂乮俁乯偺愙慄偺僌儔僼偱巭傑偭偨幰侾柤丄
丂丂丂乮係乯偺嶰妏娭悢偺僌儔僼偺搑拞傑偱偺幰俀柤丄
丂丂丂僾儕儞僩偺僌儔僼偼慡晹昤偗偨幰偑16柤
偱偟偨丅
丂丂丂嵟屻偺乽僶僀僆儕儞偺傛偆側攇宍傪昤偒丆偙傟偲帡偨攇宍傪偮偔傝側偝偄乿偵挧愴偱偒偨傕偺偼俇柤偱偟偨丅
丂乽亂俀亃憖嶌曽朄偵偮偄偰乿偺幙栤偵懳偟丄
丂丂丂乽偲偰傕傓偢偐偟偔巊偄偵偔偐偭偨乿俀柤丄
丂丂丂乽嵟弶偼偲傑偳偭偨偑丄偡偖姷傟偨乿10柤丄
丂丂丂乽偲偙傠偳偙傠傢偐傜側偐偭偨乿俆柤丄
丂丂丂乽偗偭偙偆偡偄偡偄偄偗偨乿偲俉柤
偱偟偨丅
丂亂俁亃崱擔偺侾帪娫偺庼嬈偱丄乽娭悢偺僌儔僼偵偮偄偰丄偙傟偼傢偐偭偨乿偲巚偭偨偙偲傪彂偄偰偔偩偝偄丄偲偄偆幙栤偵懳偟偰敿悢偺13柤偑摎偊偰偔傟傑偟偨丅
丂俁柤偺惗搆偑乽傛偔暘偐傜傫偐偭偨乿乽愢柧偑彮側偔偰暘偐傝偵偔偐偭偨乿乽慡晹暘偐傞傛偆側傢偐傜側偄傛偆側丒丒丒乿偲偁傝傑偟偨丅棤曉偟偰尵偊偽丄偦傟偧傟偺僌儔僼昞帵偺堄枴崌偄傪傕偭偲偪傖傫偲傢偐傝偨偐偭偨偲梫媮偟偰傞偺偩偲巚偄傑偡丅
丂乽愙揰偺栤戣偼栚偱尒偰偡偖傢偐傞偐傜傢偐傝傗偡偐偭偨乿
丂乽寁嶼偱弌偨摎偊偑偁偁傕傄偭偨傝僌儔僼偲崌偆偺偼丄堦斣嵟弶偵悢妛偺栤戣偵庢傝慻傫偱堦掕偺朄懃傪尒偮偗偨偙偲偑偡偛偄乿
丂乽嶰妏娭悢偺僌儔僼側偳帺暘偱昤偔偲搑拞偱傊傫偵側偭偰偟傑偆偗偳丄僐儞僺儏乕僞偩偲嵟屻傑偱偒傟偄偵尒傟傞偺偱偨傔偵側偭偨乿
丂乽幃偱彂偐傟傞傛傝僌儔僼偱尒偨傎偆偑傗偭傁傝傢偐傝傗偡偐偭偨丅娭悢偺曌嫮傪偡傞慜偵僐儞僺儏乕僞偺庼嬈傪傗偭偰傕傜偊偰偄偨傜丄娭悢偑岲偒偵側傟偨偐傕偟傟側偄乿
丂乽崌惉娭悢側偳偑攇傪懪偮偙偲偑暘偐偭偨乿
丂乽侾帪娫偑憗偐偭偨乿
丂晛抜偺庼嬈偺拞偱庤寉偵丄億僀儞僩揑偵娭悢僜僼僩偱昞帵偱偒偨傜丄偳傫側偵偐妝偟偄庼嬈偑偱偒傞偩傠偆偲巚偄傑偡丅
丂偙偺係丆俆擭丄乽偙偙偵僐儞僺儏乕僞偺戝夋柺偑弌偰偒偰丄僐儞僺儏乕僞偑丂僀儅僇儔y亖x^3+x^2亅1僲僌儔僼儝僇僉儅僗丂偲尵偭偰昤偄偨偲偡傞偲丒丒丒乿偲尵偄側偑傜庼嬈偡傞傛偆偵側偭偰偄傞偺偱偡偑丄壗夞偐偱傕偙偺傛偆側帇妎揑僐儞僺儏乕僞昞帵傪偝偣傟偽丄惷揑側崟斅偱偁偭偰傕惗搆偨偪偼偦偙偵摦揑側丄惍偭偨僌儔僼昞帵偺僀儊乕僕傪廳偹偰偔傟傞偲怣偠傑偡丅
丂嵟屻偺幙栤偲偟偰丄乽亂係亃僐儞僺儏乕僞偺庼嬈偼偲偆偲偆1擭娫偱1夞偟偐偱偒傑偣傫偱偟偨乿偵懳偟偰
丂丂丂乽偙傫側庼嬈偼帪乆偁偭偨傎偆偑傛偄 15柤乿
丂丂丂乽侾擭偵侾夞偖傜偄偱傛偄 俀柤乿
丂丂丂乽側偄傎偆偑傛偄 侽柤乿
丂丂丂乽偳偪傜偲傕偄偊側偄 俈柤乿
丂丂丂乽柍夞摎 侾柤乿
偲偄偆寢壥偱偟偨丅
丂偙傟傑偱偺帋峴偺忋偱丄乽悢嘨偵偍偗傞擄堈搙偺崅偄娭悢暘栰乿偵懳偟偰丄帇妎揑側僌儔僼昞帵偼丄乽巻偲墧昅乿偲偺偒偪傫偲偟偨屻晅偗偑偱偒傟偽丄棟夝搙丒嫽枴搙傾僢僾傊戝偒側岠壥傪敪婗偱偒傞偲寢榑偯偗傞偙偲偑偱偒傑偡丅
丂棃擭搙偐傜慡崙偱乽忣曬俀扨埵乿偑昁廋偲側傝丄僐儞僺儏乕僞憖嶌偵偮偄偰傕婎慴傪慡堳妛傫偱偒傑偡丅
丂偙傟傑偱偱偡偲丄僐儞僺儏乕僞偺庼嬈傪偟傛偆偲偡傟偽丄僗僀僢僠偺擖抐丄儅僂僗憖嶌丄傾僀僐儞僋儕僢僋側偳偺堄枴崌偄偐傜巒傔側偗傟偽側傝傑偣傫偱偟偨丅
丂幚嵺丄偙偺帺慠壢妛椶宆偺惗搆偨偪偼丄慡堳侾擭師偵丄廡侾帪娫偺乽忣曬婎慴乿偱丄儚乕僾儘丄昞寁嶼丄僀儞僞乕僱僢僩丄僌儔僼傿僢僋僗傪妛傫偱棃傑偟偨丅俀擭屻偺偙偺庼嬈偱傕儅僂僗偺憖嶌側偳傑偭偨偔愢柧偡傞昁梫偑偁傝傑偣傫偱偟偨丅
丂慡崙揑偵傕丄億僀儞僩揑偵庼嬈傊棙梡偱偒傞慺抧偑偱偒偰偄偔偲巚傢傟傑偡丅
係丏崱擭俈寧丄傕偆堦搙庼嬈傪偟傑偟偨
丂崱擭搙丄傢偨偟偼俁擭惗偺乽悢俠乿傪扴摉偟偰偄傑偡丅
丂俀妛婜丄栤戣廤墘廗偲暲峴偟偰乽戞俀復 偄傠偄傠側嬋慄乿傪嫵偊傑偡丅
丂乽幃偑恾宍傪憂傞乿偲戣偟偨僐儞僺儏乕僞僨儌儞僗僩儗乕僔儑儞傪帪愜傗傞偮傕傝偱偡偑丄偙偺俈寧丄峫嵏屻偺摿暿庼嬈偱丄嶐擭偲摨條偺庼嬈傪傗傝傑偟偨丅
丂嶐擭摨條丄偙偆傗丄偁偁傗偲惗搆偳偆偟偱嫵偊崌偄側偑傜丄偵偓傗偐側庼嬈偵側傝傑偟偨偑丄廔傢偭偨屻丄岥乆偵乽妝偟偐偭偨乿偲尵偭偰偔傟傑偟偨丅
丂偙偺庼嬈偱偼丄嬌尷抣傪晅偗壛偊傑偟偨丅
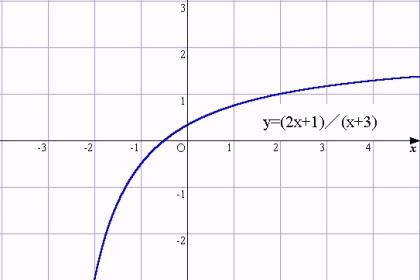
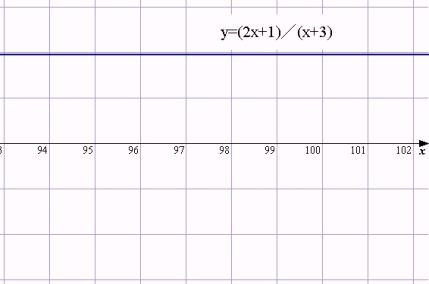
丂sin倶乛倶 偺 x仺0 偺嬌尷抣丄(2x+1)乛(x+3) 偺 x仺亣 偺嬌尷抣傪僌儔僼偱挷傋丄寁嶼偲崌抳偟偰偄傞偙偲傪妋偐傔傑偟偨丅
 丂
丂
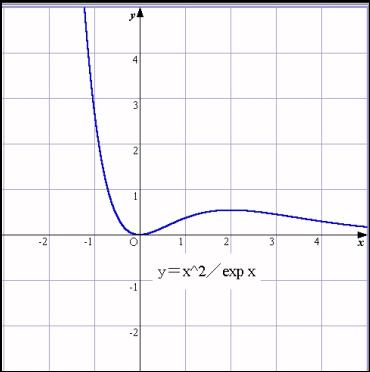
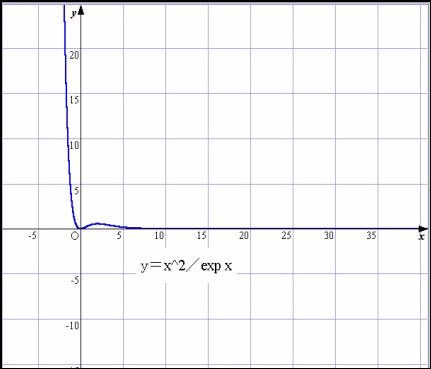
丂x偺俀忔偲 exp 偺憹偊曽偺寘偑堘偆偙偲傪帵偡 x^2乛exp倶 偺 x仺亣 偺嬌尷抣偵偮偄偰傕塃偺恾偺傛偆偵丄1乛100偵弅傔傞偙偲偱丄嬌尷抣偑侽偲側傞偙偲偑妋偐傔傜傟傑偡丅
 丂
丂
丂偦偺拞偱偙傫側応柺偵弌夛偊傑偟偨丅
丂忋弎偺俀偺(2) 偺乽y亖x+sin倶乿偺僌儔僼傪梊憐偡傞栤戣偺帪丄堦恖偺惗搆偺夋柺偑偢偄傇傫堘偭偨昞帵偵側偭偰偄傞偺偱偡丅椙偔尒偰傒傑偡偲偦偺惗搆偼丄娭悢幃傪乽y亖x+sinx乿偲偣偢偵乽y亖x丒sin倶乿偲偟偰偄傞偺偱偡丅
丂愨岲偺僠儍儞僗偱偡丅
丂乽傒傫側偪傚偭偲拲栚丅仜仜偔傫偑y亖x+sin倶偠傖側偔y亖x丒sin倶偲偟偰僌儔僼傪昤偄偰偄傑偡丅娭悢幃傪擖傟傞慜偵峫偊偰偔偩偝偄丅偳傫側僌儔僼偵側傞偲梊憐偱偒傑偡偐丅乿
丂偙傫側偲偒惗搆偨偪偼擇偮偵暘偐傟傑偡丅媍榑偟側偑傜峫偊傛偆偲偡傞惗搆丄懸偭偰偍傟偢偵偡偖娭悢幃傪擖椡偟偰寢壥傪尒傛偆偲偡傞惗搆偱偡丅屻幰偺惗搆偨偪偐傜丄乽偙傫側傗乕乿偲偄偆惡偑偁偑傝巒傔傑偡丅
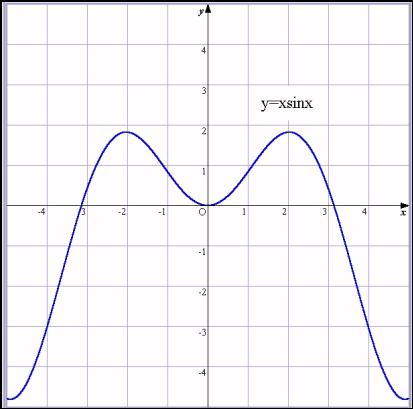
丂乽側傫偐傛偔傢偐傜傫側偁丅偠傖偁丄偳傫偳傫弅傔偰偄偭偰昞帵偝偣偰乕乿偲巜帵偟傑偡丅師偺條側僌儔僼偑晜偐傃忋偑偭偰偒傑偡丅
 丂
丂
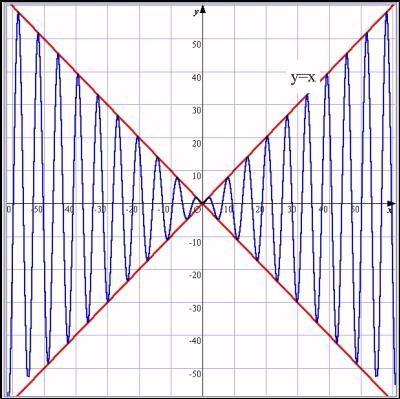
丂乽側傫偱x丒sin倶偩偲偙偆側傞傫傗傠乿偲栤偄偐偗傑偡丅
丂乽怳摦傗丅乿偲偄偆摎偊丅
丂乽偦偆側傫偱偡丅y亖x偵懳偟偰僾儔僗偲儅僀僫僗偵怳摦偑偍偍偄偐傇偝偭偰偄傞偺偱偡丅乿偲堄枴崌偄偑偮偗傜傟傑偟偨丅
丂偡偖偵僌儔僼昞帵偱偒傞偙偲偑丄偙偺傛偆側巚傢偸庼嬈揥奐傪惗傒傑偟偨丅
丂崟斅庼嬈偵栠偭偨偲偒丄偙偺偙偲傪巚偄弌偝偣偰丄乽偝偁丄偙偺娭悢幃偱偳傫側恾宍偑偱偒傞偱偟傚偆乿偲栤偄偐偗偨帪丄惗搆偨偪偼僐儞僺儏乕僞偺戙傢傝偵丄摢偱悇棟傪巒傔偰偔傟傞偱偟傚偆丅
丂俀妛婜偺庼嬈偑妝偟傒偱偡丅